Оси ординат и абсцисс, Ось ординат – кратко что это такое?
Координаты — это набор данных, по которому определяется положение того или иного объекта. Шаг 1 из 2. В декартовой системе координат, где ось абсцисс направлена по … Википедия Циссоида Диоклеса — Циссоида Диокла плоская алгебраическая кривая третьего порядка. А 0;3 : 0 — «подпрыгнули» на месте, 3 — вверх. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии , проверенной 11 января года; проверки требует 1 правка.
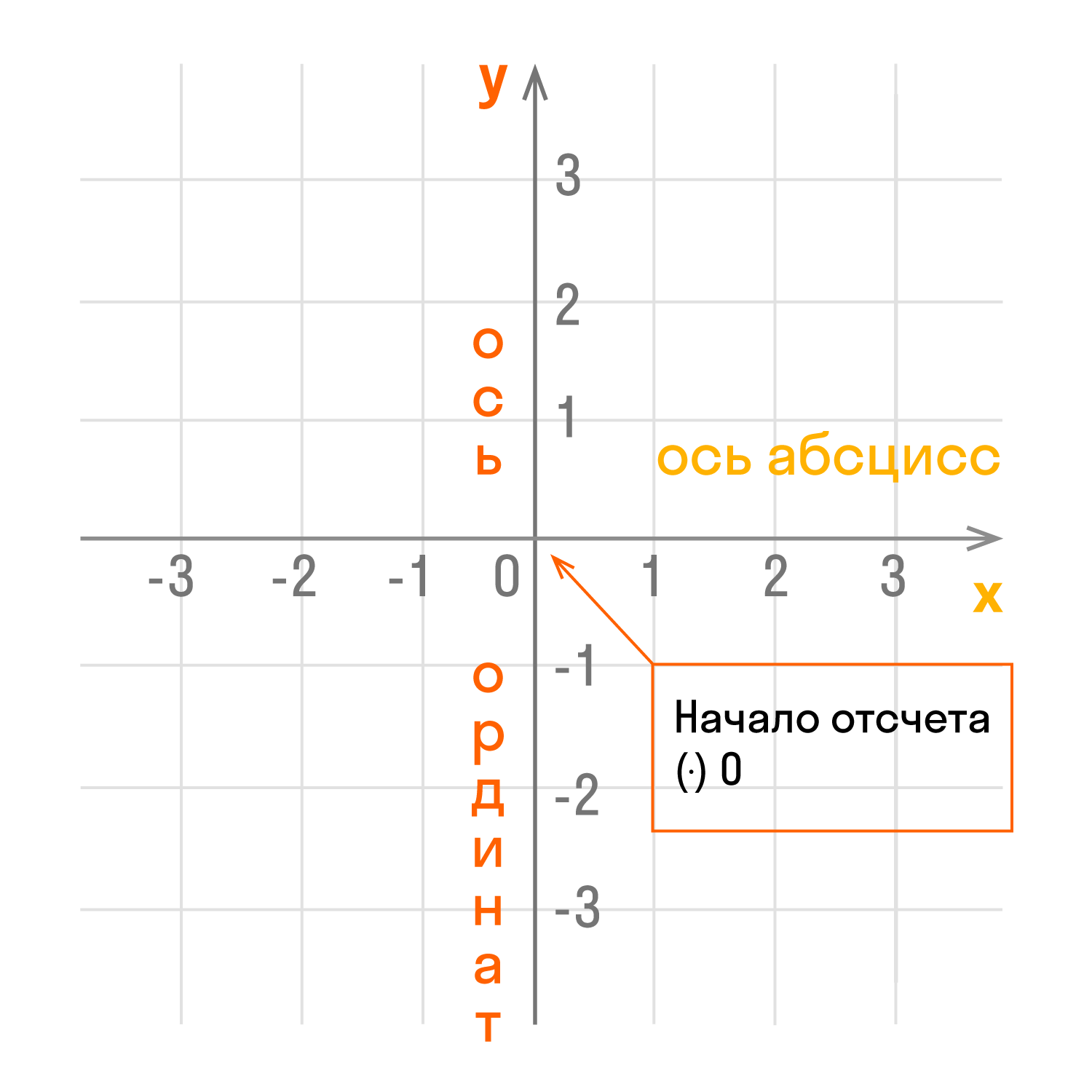
Так высчитывают координаты точки в составе графика. По факту оси можно называть как угодно. Это зависит только от ученика, решающего задачу. А названия абсцисс и ординат сохраняется всегда. Осью абсцисс зовется ось х. Она отвечает за отслеживание горизонтальных перемещений точки.
В переводе с латинского языка «абсцисса» переводится как «отрезок». Если говорить кратко о оси ординат, то так зовется ось у. Эта ось отвечает за перемещения по вертикали.
Если точка поднимается или опускается, это можно отследить по изменению ординаты.
Ордината переводится как порядок. Если воспользоваться переводом, то можно сказать так: чтобы отметить точку в системе координат, нужно отложить отрезок по горизонтали, равный абсциссе и поднять точку на несколько порядков вверх по ординате.
Так проще запомнить правильные названия осей. Мы поговорили о Декартовой системе координат. Узнали, зачем нужно использовать правильные названия осей. Поговорили о том, что такое абсцисса и ордината. Выяснили, почему чаще всего оси обозначаются х и у.
Сказали о том, что традиционное обозначение может быть заменено в любой момент. Ось ординат. Средняя оценка: 4. Что мы узнали? Начало отсчета. Единичные отрезки. Обычно по умолчанию стараются использовать правые координатные системы, а при их графическом изображении ещё и располагают их, если можно, в одном из нескольких обычных традиционных положений.
На рис. Правую и левую системы координат невозможно поворотами [9] совместить так, чтобы совпали соответствующие оси и их направления. Определить, к какому классу относится какая-либо конкретно взятая система координат, можно, используя правило правой руки, правило винта и т. Любая из восьми областей, на которые пространство делится тремя взаимно перпендикулярными координатными плоскостями, называется октантом. Прямоугольная система координат может быть использована и в пространстве любой конечной размерности аналогично тому, как это делается для трехмерного пространства.
Для обозначения координат обычно [10] применяют не разные буквы, а одну и ту же букву с числовым индексом. Чаще всего это:. В любой размерности пространства прямоугольные координатные системы делятся на два класса, правые и левые или положительные и отрицательные. Для многомерных пространств какую-то одну из координатных систем произвольно условно называют правой, а остальные оказываются правыми или левыми в зависимости от того, той же они ориентации или нет [11].
Для определения прямоугольных координат вектора применимых для представления векторов любой размерности можно исходить из того, что координаты вектора направленного отрезка , начало которого находится в начале координат, совпадают с координатами его конца [12]. Для векторов направленных отрезков , начало которых не совпадает с началом координат, прямоугольные координаты можно определить одним из двух способов:.
Это верно для любой размерности n и даже, наравне с прямоугольными, для косоугольных координат. Внешнее произведение :. Прямоугольная система координат [13] любой размерности также описывается [14] набором ортов единичных векторов , сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу. Такие орты образуют ортонормированный базис , притом [15]. При этом в случае правой системы координат действительны следующие формулы с векторными произведениями ортов:.
Для размерностей пространства более 3, или для общего случая, когда размерность может быть любой обычно для ортов применяют вместо этого обозначения с числовыми индексами, достаточно часто [16] это:.
Материал из Википедии — свободной энциклопедии. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии , проверенной 11 января года; проверки требует 1 правка.
Прямоугольная декартова система координат. Основной источник: [1]. Раздел VI. Выгодский, под ред. Analytic geometry неопр.
Дата обращения: 6 августа Архивировано 6 августа года. Linear Algebra Done Right - Springer. Если да, то данная система считается правой, если нет, то левой.
Ещё проще технически это выяснить через знак определителя матрицы преобразования от правого базиса к данному.