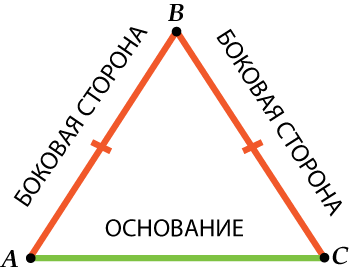
Боковые стороны равнобедренного треугольника
Угол в вершине равен 30 градусов, синус этого угла равен одной второй. Почему я об этом специально говорю? Все эти формулы есть в Википедии, можно их отыскать и в разных математических справочниках.
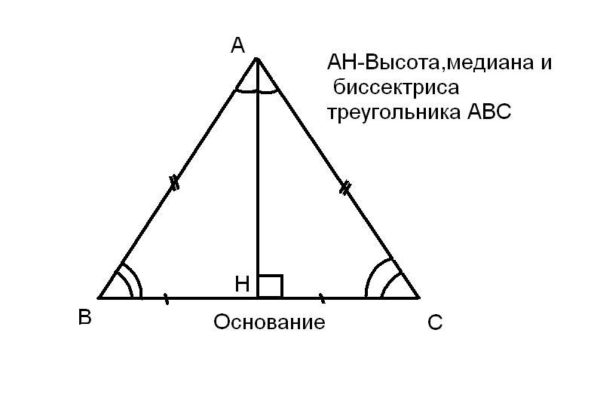
Высота, медиана, биссектриса равностороннего треугольника.
Биссектриса произвольного треугольника. Биссектриса прямоугольного треугольника. Медиана произвольного треугольника.

Медиана прямоугольного треугольника. Все формулы по геометрии.
Радиус вписанной, описанной окружности. Окружность и круг.
Текстовые задачи Движение по прямой Движение по окружности Движение по воде Работа Смеси, сплавы Проценты, прогрессии Графики функций Прямые Параболы Гиперболы Корни Логарифмические функции Показательные функции Тригонометрические функции Пересечения графиков Модули Исследование функций Степенные функции Дробно-рациональные функции Исследование без производной Сложные уравнения Тригонометрические уравнения Тригонометрические уравнения с учетом ОДЗ Показательные уравнения Смешанные уравнения Стереометрия Неравенства Экономические задачи Планиметрия Параметры Теория чисел.
У нас есть площадь равнобедренного треугольника и угол при его вершине. Нужно найти длину боковой стороны. Можно использовать теорему Пифагора, тригонометрические функции и всё то, чему вас учили до этого момента.
Используя разные трюки с подстановками, можно в конце концов найти решение этой задачи.
Я поступлю гораздо проще. Для определения площади треугольника существует много разных формул.
Вот к ним-то я и предлагаю присмотреться внимательнее. Все эти формулы есть в Википедии, можно их отыскать и в разных математических справочниках.

Шестая формула нам подходит как нельзя кстати. Здесь площадь треугольника определяется по боковой стороне и углам. Зная площадь треугольника, можно легко найти сторону. Осталось только с углами разобраться. Углы в основании равнобедренного треугольника равны.
На картинке запишем те условия, которые превращают обычный треугольник в равнобедренный. Как видите, нам даже нет необходимости искать углы в основании равнобедренного треугольника — синусы этих углов равны и сокращаются в дроби. Угол в вершине равен 30 градусов, синус этого угла равен одной второй. Теперь легко можно решить задачу. Выражаем квадрат стороны через площадь и синус угла в вершине, извлекаем квадратный корень и получаем сторону размером в 10 единиц.
Это взрослое решение. Все взрослые пользуются справочниками, не вдаваясь в подробности. Для инквизиторов от математики такое решение может показаться богохульством. Специально для инквизиторов мы сейчас выведем формулу площади равнобедренного треугольника через боковую сторону и синус угла в вершине.

Как и предыдущее решение, это будет пример того, как нужно пользоваться математикой. Я обещал писать в режиме реального времени. Так вот, всё, что написано до сих пор, писалось в ночь с пятницы на субботу. Сейчас утро воскресенья.